算法笔记：最短路径

• 迪杰斯特拉（Dijkstra）算法

   1 #define MAXVEX 9
   2 #define INFINITY 65535
   3 typedef int Pathmatrix[MAXVEX]; // 用于存储最短路径下标的数组
   4 typedef int ShortPathTable[MAXVEX]; // 用于存储到各点最短路径的权值和
   5 // Dijkstra算法，求有向网G的v0顶点到其余顶点v最短路径P[v]及带权长度D[v]
   6 // P[v]的值为前驱顶点下标，D[v]表示v0到v的最短路径长度和
   7 void ShortestPath_Dijkstra(MGraph G, int v0, Pathmatrix *P, ShortPathTable *D) {
   8     int v, w, k, min;
   9     int final[MAXVEX]; // final[w]=1表示求的顶点v0至vw的最短路径
  10     for (v = 0; v < G.numVertexes; v++) { // 初始化数据
  11         final[v] = 0; // 全部顶点初始化为未知最短路径状态
  12         (*D)[v] = G.matrix[v0][v]; // 将与v0点有连线的顶点加上权值
  13         (*P)[v] = 0; // 初始化路径数组P为0
  14     }
  15     (*D)[v0] = 0; // v0至v0路径为0
  16     final[v0] = 1; // v0至v0不需要求路径
  17     // 开始主循环，每次求得v0到某个v顶点的最短路径
  18     for (v = 1; v < G.numVertexes; v++) {
  19         min = INFINITY; // 当前所知离v0顶点的最近距离
  20         for (w = 0; w < G.numVertexes; w++) { // 寻找离v0最近的顶点
  21             if (!final[w] && (*D)[w]<min) {
  22                 k = w;
  23                 min = (*D)[w]; // w顶点离v0顶点更近
  24             }
  25         }
  26         final[k] = 1; // 将目前找到的最近的顶点设置为1
  27         for (w = 0; w < G.numVertexes; w++) { // 修正当前最短路径及距离
  28             // 如果经过v顶点的路径比这条路径的长度短的话
  29             if (!final[w] && (min+G.matrix[k][w]<(*D[w])) { // 说明找到了更短的路径，修改D[w]和P[w]
  30                 (*D)[w] = min + G.matrix[k][w]; // 修改当前路径长度
  31                 (*P)[w] = k;
  32             }
  33         }
  34     }
  35 }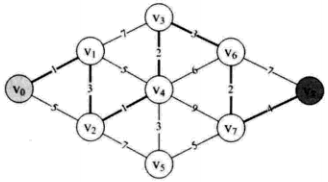

  

• 弗洛伊德（Floyd）算法
  （还没学）