https://leetcode.cn/problems/symmetric-tree/

题面

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

img

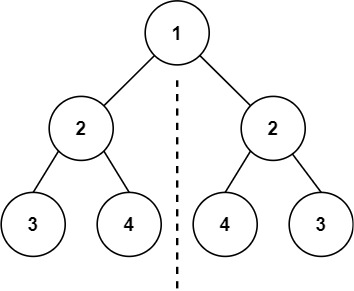
1
2
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

img

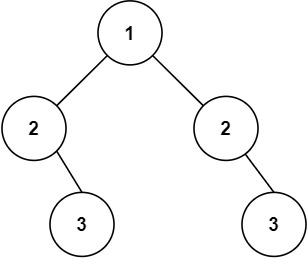
1
2
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

  • 树中节点数目在范围 [1, 1000] 内
  • -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

思路

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool compare(TreeNode* left, TreeNode* right) {
    // 首先排除空节点的情况
    if (left == NULL && right != NULL) return false;
    else if (left != NULL && right == NULL) return false;
    else if (left == NULL && right == NULL) return true;
    // 排除了空节点，再排除数值不相同的情况
    else if (left->val != right->val) return false;
    
    // 此时就是【左右节点都不为空，且数值相同】的情况
    // 此时才做递归，做下一层的判断
    bool outside = compare(left->left, right->right);
    bool inside = compare(left->right, right->left);
    return outside && inside;
}
bool isSymmetric(TreeNode* root) {
    if (root == NULL) return true;
    return compare(root->left, root->right);
}

迭代

注意：这里的迭代法和前中后序遍历的迭代法不一样，因为这道题的本质是判断两棵树是否是相互翻转的，已经不是所谓二叉树遍历的前中后序的关系了。

这里可以用队列（用栈也可以）来比较根结点的左右子树是否相互翻转。（注意这不是层序遍历）

使用队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool isSymmetric(TreeNode* root) {
    if (root == NULL) return true;
    queue<TreeNode*> que;
    que.push(root->left); // 将左子树头节点加入队列
    que.push(root->right); // 将右子树头节点加入队列
    
    while (!que.empty()) { // 判断这两棵树是否相互翻转
        TreeNode* leftNode = que.front(); que.pop();
        TreeNode* rightNode = que.front(); que.pop();
        
        // 左节点为空、右节点为空，此时是对称的
        if (!leftNode && !rightNode)
            continue;
        // 左右其中一个节点不为空，或者都不为空但数值不相同，返回false
        if (!leftNode || !rightNode || leftNode->val != rightNode->val)
            return false;
        
        que.push(leftNode->left);
        que.push(rightNode->right);
        que.push(leftNode->right);
        que.push(rightNode->left);
    }
    return true;
}

使用栈

可以发现这个迭代法其实是把要比较的左右两个子树的元素顺序放进一个容器，然后成对取出进行比较，那么其实使用栈也是可以的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool isSymmetric(TreeNode* root) {
    if (root == NULL) return true;
    stack<TreeNode*> st; // 改用栈
    st.push(root->left);
    st.push(root->right);
    while (!st.empty()) {
        TreeNode* leftNode = st.top(); st.pop();
        TreeNode* rightNode = st.top(); st.pop();
        
        if (!leftNode && !rightNode)
            continue;
        if (!leftNode || !rightNode || leftNode != rightNode)
            return false;
        
        st.push(leftNode->left);
        st.push(rightNode->right);
        st.push(leftNode->right);
        st.push(rightNode->left);
    }
    return true;
}